Платежеспособность страховщика или перестраховщика - это объективный показатель его текущего финансового состояния путем прогнозирования в будущем. Иначе говоря, это возможность выполнения в будущем его обязательств благодаря тем активам, которые есть в распоряжении перестраховщика, представляют собой реальные ценности, и поэтому являются ликвидными.
Экономическая оценка рисков и капитала заставит страховщиков и перестраховщиков применять экономические принципы при подсчете имеющегося и необходимого капитала. О том, что готовят международные стандарты платежеспособности Solvency II для страховых рынков мы писали еще в 2008 году, сегодня мы коснемся практического применения Стандартной формулы.
Подход, основанный на экономических принципах, определяется применением рыночных стоимостей для оценки как активов, так и пассивов, отображенных в балансах страховщиков. Учитывая каждую конкретную ситуацию, каждый перестраховщик или страховщик должен определить, будет ли он использовать Стандартную формулу Solvency II или, в качестве альтернативы, частичную внутреннюю модель или полностью внутреннюю модель для таких расчетов. Можно ожидать, что некоторые компании будут опираться на Стандартную формулу после внедрения стандартов Solvency II. В то время как Стандартная формула имеет много сильных сторон, есть несколько моментов, в которых она может быть усовершенствована.
Необходимый уровень капитала может рассматриваться как вторая линия защиты платежеспособности страховой компании и ее страхователей. Первая линия защиты - беспрерывное управление риском. Если проблемы в отдельной компании имеют развитие, они не могут быть предупреждены за счет риск-менеджмента, тогда нужен капитал для покрытия финансовых потерь, которые возникли. Из этого следует, что для органа надзора для удовлетворения низшей суммой требований к капиталу при специфическом подходе к компании, нужны гарантии, что определенный источник риска под контролем, его влияние значительно снижено, а потому требования к капиталу могут быть низшими. Поэтому, при одобрении использования компанией усовершенствованного или специфического подхода, орган надзора должен подтвердить, что компания использует надлежащие процессы риск-менеджмента вместе с надлежащей структурой отчетности.
Так называемые Исследования количественного влияния (QIS), с помощью которых отрасль готовится к переходу к новым требованиям к капиталу, показывают, что договора пропорционального перестрахования полностью отображены в Стандартной формуле, которая ведет к соответствующим снижениям требований к платежеспособности капитала (SCR).
Если взять непропорциональное перестрахование договора эксцедента ущерба, при использовании Стандартной формулы, не отображают соответствующего эффекта снижения риска в регуляторных целях, поскольку экономические выгоды от таких договоров не полностью отображаются Стандартной формулой. Как вывод, требования к платежеспособному капиталу могут быть или переоцененные или недооцененные.
Стандартная формула Solvency II
Третьей Директивой Solvency II ЕС создал современную, чувствительную к рискам основу регулирования страхования. Считается, что новая структура будет иметь значительное влияние и значительно изменит условия страхования в Европе. Европейский страховой рынок, в частности СЕА (Европейский комитет страховщиков) и Форум исполнительных риск-менеджеров (CRO) поддерживают новые условия, которые будут полностью введены в конце 2012 года.
Используемая сейчас модель Solvency I учитывает лишь страховой риск при определении требований к капиталу страховщика. Другие риски, такие как рыночный и кредитный, не учитываются. Кроме того, режим Solvency I имеет определенные ограничения относительно учета перестрахования для снижения требований к капиталу. Учет non-life перестрахования ограничен 50% коэффициентом удержания (определяется как средние чистые заявленные убытки в процентном отношении к среднему валовому заявленному ущербу).
Учитывая то, что режим Solvency I не учитывал то, что компании могут пострадать вследствие риска естественных катастроф или рыночного риска, эти риски учтены стандартом Solvency II, что может привести к значительному увеличению требований к платежеспособности капитала (SCR). С другой стороны, хорошо диверсифицированный портфель активов и пассивов может вызвать эффект диверсификации, который приводит к снижению SCR.
Стандартная формула разработана таким образом, чтобы ее можно было применить для всех страховщиков и перестраховщиков, а регулятор мог бы использовать Стандартную формулу как точку отсчета для внутренних моделей во время сертификации. Кроме того, регуляторы могут требовать от компаний, при применении утвержденной внутренней модели, также использовать Стандартную формулу (не обязательно лишь во время начальной фазы на протяжении 2-х лет после внедрения режима Solvency II, как предложено Комиссией ЕС в проекте директивы).
Переход на Solvency ІІ является переходом к экономической, построенной на риске модели регулирования: этот проект не только имеет цель усовершенствовать техники риск-менеджмента страховщиков, он также должен создать условия, которые бы более точно отображали риски, которые создают страховщики. Solvency II будет иметь существенное влияние на стоимостные показатели отрасли, в частности на требования к капиталу. Тем не менее, конечная выгода для отрасли и потребителей будет зависеть от завершения мероприятий по внедрению, которые пока дорабатываются Комиссией ЕС.
Взгляд на non-life риски в Стандартной формуле
В контексте QIS, Стандартная формула рассчитывает платежеспособность капитала (SCR) как сумму цифр риска капитала для андеррайтингового, рыночного, банкротства партнеров и операционного рисков и их соответствующих модулей SCR.
Структура платежеспособности капитала (SCR) для non-life и ее влияние на перестрахование
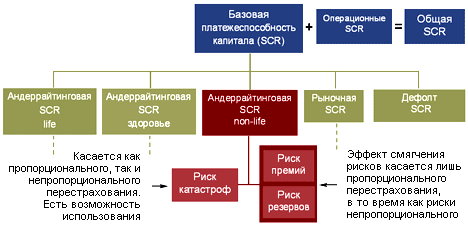
В отношении к перестрахованию, Стандартная формула имеет определенные недостатки, которые не поощряют к адекватному риск-менеджменту. Договора пропорционального перестрахования могут быть учтены в Стандартной формуле полностью, тем самым, снижая SCR. В отличие от этого, договора непропорционального перестрахования учитываются неполной мерой, поэтому страховые компании часто не получают адекватного отображения капитала при непропорциональном перестраховании. Это происходит из-за того, что Стандартная формула использует логарифмически нормальное распределение, которое не разрешает нормально учитывать нелинейные риски.
Есть несколько способов преодоления неадекватного учета непропорционального перестрахования. Вместо использования Стандартной формулы страховщики могут использовать полностью или частично внутреннюю модель, которая будет показывать более реалистические результаты. Это разрешит более реалистически рассматривать непропорциональное перестрахование в специфическом контексте стоимости и выгоды.
Комиссия ЕС может разработать пересмотренный подход относительно непропорционального перестрахования, который разрешит более гибко использовать эффект снижения риска.
Влияние непропорционального перестрахования в Стандартной формуле
Описание того, каким образом непропорциональное перестрахование смягчает риски, приведено в форме таблицы.
Для non-life бизнеса в Стандартной формуле перестрахования имеет эффект снижения риска для:
- риска премий за отдельным направлением бизнеса;
- риска резервов за линией бизнеса;
- риска естественных катастроф.
Стандартная формула объединяет риск премий и резервов в один модуль SCR для non-life андеррайтингового риска, а другим модулем SCR является катастрофический риск. Эффект снижения риска за счет перестрахования ведет к снижению андеррайтингового SCR, базового SCR и общего SCR.
Перестраховочный эффект катастрофических рисков может быть учтен без ограничений. Кроме этого существует возможность оценки катастрофического риска согласно стандартизированному методу, описанному в технической спецификации. В этом случае эффект перестрахования будет учтен путем вычитания полного покрытия (учитывая восстановление) непропорционального перестрахования из валовой суммы обязательств.
Другой подход используется для риска премий и резервов, со стандартным отклонением и функцией отклонения. Страховые премии и резервы рассматриваются как базовые факторы, на которые распространяется нормальная логарифмическая логика распространения. Наилучший результат дает объединение суммы премии и резервов.
Стандартное отклонение (σ) рассчитывается как среднее значение стандартных рыночно-ориентированных отклонений для риска премий и резервов за каждой бизнес-линией.
Показатели рассчитываются как премии и соответственно резервы для каждой бизнес-линии. Эффект потенциального отклонения через географическую диверсификацию рассчитывается исходя из географического происхождения премий и резервов, и считается дисконтным от общих показателей объемов.
Таким образом SCR для риска премий и резервов (NLpr) рассчитывается как:
NLpr = V*p(σ),
где p(σ) принимает нормальное распределение основного риска, p(σ) ≈ 3* σ
Пропорциональное перестрахование может рассматриваться как пропорционально снижающее основной риск, а значит и требования к платежеспособности капитала для риска премий и резервов.
Если вводятся специальные условия, такие как, лимиты на события, годовой агрегатный лимит, участие в прибылях и ущербе или условия замены, то они не могут соответствующим образом быть учтены.
Отдельные риски не всегда принимаются во внимание из-за своих объемов, т.е. непропорциональное перестрахование разницы между валовой и чистой стоимостью перестрахования, которое лучше всего отображает ущерб, который покрывался отдельным контрактом, тем не менее, не покрывают долгосрочные события.
QIS4 разрешает цеденту использовать индивидуальные стандарты отклонения для риска премий, которые базируются на его истории коэффициента чистого ущерба. Увы, такой подход не является гибким, учитывая изменения портфеля, такие как изменения структуры перестрахования, а потому, во многих случаях, не может быть примененным.
Уменьшение риска путем непропорционального перестрахования
Непропорциональное перестрахование - очень гибкий инструмент снижения риска, который разрешает переносить определенную долю риска со страховщика на перестраховщика соответственно склонности страховщика к риску. Чаще всего этот инструмент используется для передачи пиковых нагрузок, например для защиты от катастрофического риска, так называемые катастрофические договора эксцедента убытка (Cat XL).
Договора эксцедента убытка часто используются для гражданской ответственности автовладельцев. Типичный договор эксцедента убытка может определяться приоритетом, покрытием или количеством выплат. Другим видом непропорционального перестрахования являются договора эксцедента убыточности, которые определяют приоритет годового ущерба и покрывают избыточный ущерб.
Из-за своей гибкости, моделирование непропорционального перестрахования сложнее, чем для пропорционального. В отличие от пропорционального перестрахования тарифы на непропорциональные договора связаны не с премиальным доходом цедента, а с ожидаемыми возможными выплатами по контракту.
Таким образом, полная оценка эффекта снижения риска путем непропорционального страхования требует статистики по отдельному убытку. Тем не менее, из-за отсутствия таких данных наперед, оценки должны быть сделаны на основе распределения ущерба и частоты их наступления. За этим предположением тариф будет рассчитываться исходя из средней структуры ущерба (ожидаемые потери).
Такой подход не учитывается Стандартной формулой, которая рассматривает цену перестрахолвания, как основную меру эффекта снижения риска при непропорциональном перестраховании.
Сравнение учета Стандартной формулой снижения риска для разных типов риска
| . | Риски | Эффект снижения риска | |
|---|---|---|---|
| . | По «поддаванию» риску (показатели объемов) | По стандартным отклонениям | |
| . | Риск премий | Страховщик предоставляет чистые премии (показатели объема). В отличие от пропорционального перестрахования эффект экономического снижения риска лучший для непропорционального перестрахования по долгосрочному периоду, а не по периоду наилучшей выборки. Этот аспект нивелируется Стандартной формулой. | Индивидуальные стандарты отклонений учитываются, если цедент предоставляет историю убыточности за последние 7 лет (достоверный подход). Этот метод приемлемый лишь тогда, когда перестраховочная программа была постоянной на протяжении последних лет. |
| . | Риск резервов | Страховщик предоставляет чистые резервы (показатели объема). Эффект снижения риска зависит в значительной степени от политики резервирования, тем не менее перестрахование может также защищать от значительных отрицательных результатов. | Сущность конкретных стандартных отклонений не была принята во внимание для SCR расчета, хотя они могут быть предоставлены для Стандартной формулы QIS. |
| . | Риск катастроф | В зависимости от избранного метода, эффект снижения риска может быть учтен Стандартной формулой полностью, например, если разрешено использование внутренних моделей | |
Практические примеры
Для иллюстрирования оценок можно привести три примера с разными типами перестрахования для типичного портфеля. Чтобы показать разницу в оценке эффекта перестрахования, сравним нагрузки рискового капитала для страховых премий до и после перестрахования, как это используется в Стандартной формуле. В качестве примера внутренней модели приводится модель Ricasso.
Описание примеров
Типичный портфель состоит из полисов гражданской ответственности автовладельцев. Ожидаемый объем премий - $100 млн. Можно ожидать, что небольшой ущерб будет иметь высокую частоту наступления, а большие - малую, например телесные повреждения.
Кумулятивный годовой ущерб может быть смоделирован с помощью кривой статистической частоты ущерба. Исходя из предположений, что стандартное отклонение составляет 9%, а ожидаемые премии в размере $100 млн. - это наилучшие ожидания, рассчитываем влияние следующих типов перестрахового покрытия:
- Пример 1 - QS (Quota Share) - 50% квотная доля. Перестраховочная комиссия на уровне начальной цены.
- Пример 2 - SL (Stop Loss) - договор эксцедента убыточности с приоритетом 120% и покрытием на $100 млн. Цена перестрахования $2 млн.
- Пример 3 - XL (Excess of Loss) - договор эксцедента убытка со следующим покрытием: 2 xs $3 млн., неограниченное восстановление (основной XL на риск); 25 xs $5 млн., без восстановления. Стоимость перестрахования составляет $8 млн.
Пример 1. QS программа (Quota Share)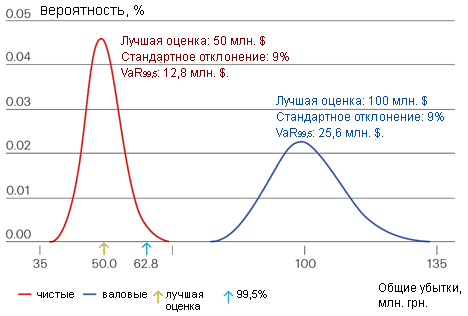
Пример 2. SL программа (Stop Loss)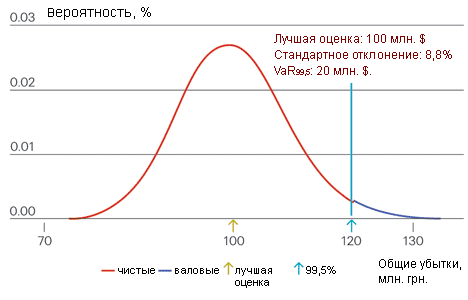
Пример 3. XL программа (Excess of Loss)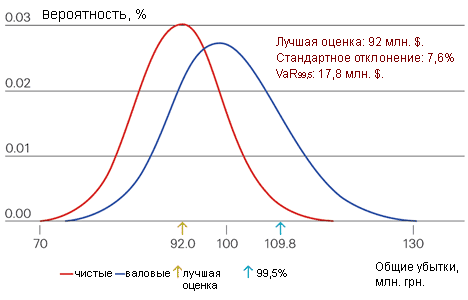
Итоги трех примеров
| $ млн. | Стандартная модель | Внутренняя модель | |||||
|---|---|---|---|---|---|---|---|
| Валовые | Чистые | Перестрахование | Валовые | Чистые | перестрахование | ||
| 1 | QS | 25,6 | 12,8 | 12,8 | 25,6 | 12,8 | 12,8 |
| 2 | SL | 25,6 | 25,1 | 0,5 | 25,6 | 20,0 5,6 | |
| 3 | XL | 25,6 | 23,5 | 2,1 | 25,6 | 17,8 | 7,8 |
Выводы
Результаты показывают, что индивидуальная рисковость ситуации не всегда соответственно учитывается, особенно в случае непропорционального перестрахования. Для договора эксцедента убытка облегчения требований к капиталу значительно выше при использовании внутренней модели, чем Стандартной формулы. При эксцеденте убытка, применение внутренней модели также дает значительно меньшие требования к капиталу.
Стандартная формула разрешает использовать специфические для компании параметры, тем не менее, с двумя ограничениями:
- она негибкая, поскольку базируется на исторических результатах, а потому может применяться лишь при стабильном портфеле и постоянной программе перестрахования;
- предположение относительно логнормального распределения может быть несоответствующим для определенных рисков. Например, для портфеля, который защищен договором непропорционального перестрахования. Это означает, что эффект снижения риска для некоторых типов перестрахования учитывается лишь частично.
Стандартная формула не может полностью учитывать эффект снижения риска за счет непропорционального перестрахования. Это, в свою очередь, противоречит фундаментальным целям системы Solvency ІІ, которые должны обеспечить целостную картину реального экономического окружения, включая все соответствующие инструменты снижения риска. В целом, эффект непропорционального перестрахования более тяжело оценить из-за его разносторонности и непредсказуемости развития программ перестрахования со временем. Как следствие, требования к платежеспособному капиталу могут быть переоценены или недооценены Стандартной формулой, что хорошо видно из примеров.
Определение перестрахования отличается для риска премий и риска резервов:
- Для риска премий можно сделать предположение относительно эффекта снижения риска, тем не менее, тяжело высчитать индивидуальные стандартные отклонения. Для этого нужно, чтобы программы перестрахования были постоянными на протяжении нескольких лет. Исторически коэффициент убыточности не очень красивый показатель для прогнозов, даже в целом по портфелю.
- Риск резервов также зависит от политики резервирования, которая учитывает взвешенный эффект снижения риска за счет разных программ перестрахования. Тем не менее, перестрахование может предоставить дополнительную защиту в случае неблагоприятных событий, например поздние требования или выявленные риски.
Как следствие проблемы, которая описана выше, любое потенциальное решение должно быть компромиссом между более сложной моделью с учетом индивидуальных стандартов отклонения, внедрение которой требует почти таких же усилий, как частичная внутренняя модель, и, с другой стороны, простоя в использовании Стандартной формулой со своими недостатками.
Стандартная формула уже сейчас довольно сложная, тем не менее, она может рассматриваться как подготовительный шаг к переходу на частичную или полную внутреннюю модель. Такое предположение имеет смысл, поскольку параметры, которые используются в Стандартной формуле, базируются на «среднем европейском страховщике» и не обязательно подходят каждой компании.
Частичная или полная внутренняя модель основана на разных принципах, включая стохастические факторы риска и индивидуальную корреляцию, будет давать более точную оценку требований к платежеспособному капиталу. Внутренняя модель оценивает специфический профиль риска компании, из-за того, что она может учитывать настоящее стандартное отклонение и корреляцию, а также индивидуальные сценарии угроз.
Использование Стандартной формулы приемлемо для многих компаний для расчета регуляторного капитала, тем не менее, страховщикам рекомендуется удержаться от ее использования с целью регулирования собственного бизнеса, ведь риск-менеджмент каждой компании должен быть индивидуальным.
Рекомендации
Исходя из каждой конкретной ситуации, страховая или перестраховочная компания должна определиться использовать ей Стандартную формулу, частичную или полную внутреннюю модель.
Чем больше компания, и чем сложнее ее бизнес, тем более приемлемой для нее является использование частичной или полной внутренней модели. Компании, которые используют Стандартную формулу, должны четко осознавать все присущие ей недостатки.
Можно ожидать определенное усовершенствование Стандартной формулы на протяжении проведения исследования количественного влияния, которое можно ожидать в 2010 году, путем использования специфических параметров или факторов приспособления. Таким образом, эффективность Стандартной модели может быть повышенная. Страховщики и перестраховщики будут продолжать следить за развитием системы и сравнивать результаты, полученные с использованием внутренних моделей и Стандартной формулы с целью определения приемлемости каждой из них.
Скачать PDF-версию обзора  Стандартная формула Solvency II в non-life перестраховании (287.06 КБ)
Стандартная формула Solvency II в non-life перестраховании (287.06 КБ)
__________________________________
Обзор опубликован в журнале "Страхова справа" №2(34)2009 и базируется на основе отчета компании Swiss Re "Focus report: Solvency II Standard Formula"




